Nominal Ordinal Interval Ratio. These are the names of the 4 types of data in statistics.
We've delved into each of these types of measurement scale individually in other posts (more on that below), but do you know how they stack up in comparison with each other?
If you don't know the differences between Interval vs Ratio data, or Ordinal vs Nominal Data, then you're in the right place.
Here is our guide to the differences between each of the 4 types of measurement scale in statistics and how to deal with each of them...
More...
Disclosure: we may earn an affiliate commission for purchases you make when using the links to products on this page. As an Amazon Affiliate we earn from qualifying purchases.
This post forms part of a series on the 4 types of data in statistics.
For more detail, choose from the options below:
4 Types of Data in Statistics: Introduction

Pin it for later
Need to save this for later?
Pin it to your favourite board and you can get back to it when you're ready.
Nominal Ordinal Interval Ratio: Measurement Scales Compared
In my experience, few people know and understand the differences between the Nominal, Ordinal, Interval, Ratio measurement scales, and as a result struggle to get to grips with what they can and can't do with their data.
That's a shame, because if you know the differences between Ordinal and Nominal data and between Interval and Ratio data, you know:
In short, if you know your Ordinal vs Nominal and your Interval vs Ratio, you have a roadmap to doing your entire study properly.
They really are that important!
Hopefully, by now you have a good understanding of what Ratio, Interval, Ordinal, Nominal measurement scales are individually. In this post we're going to take a look at the differences between them so you know what you can - and can't - do with them.
3 Simple Questions...
What's Stopping You Reaching
YOUR Data Ninja Potential?
Answer 3 questions and we'll recommend the best route to
super-charge your data career
Nominal Ordinal Interval Ratio: Mathematical Features
We begin by taking a look at the mathematical features of Nominal vs Ordinal measurement scales, and Interval vs Ratio measurement scales to see if we can spot any patterns in what you can and can't do with them.
Nominal vs Ordinal: Maths
Nominal and Ordinal data are types of Qualitative measurement scales (also known as categorical data), and you cannot perform any mathematical operations on Nominal and Ordinal data.
For each, you can say that data points are the same or different.
For example, you can say that a Pig is the same as another Pig, but is different to a Goat. A T-shirt graded as 'Small' goes into the same category as other Small T-shirts, but into a different category to those graded as Medium or Large.
Where Nominal and Ordinal data differ is that Ordinal categories are ordered, so you can label categories as Greater Than or Less Than other categories.
For example, a 'Medium' T-shirt is Larger Than a 'Small', but is Smaller than a 'Large' T-shirt.
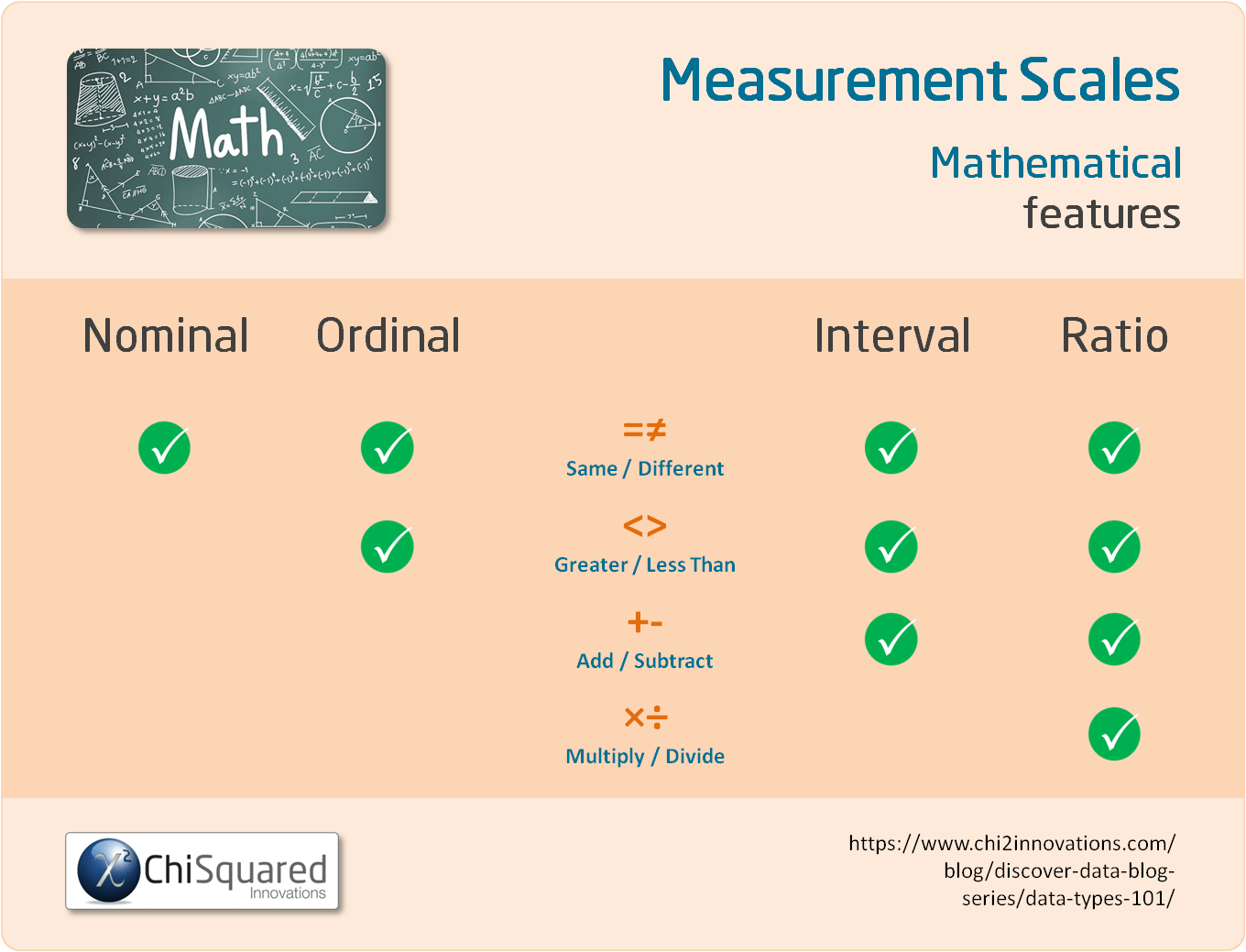
Interval vs Ratio: Maths
Interval and Ratio data are types of Quantitative measurement scales (also known as numerical data), and you can perform a variety of mathematical operations on Interval and Ratio data.
In common with Ordinal data, with Interval and Ratio data you can make simple comparison, such as Same/Different and Greater/Less Than.
With Interval and Ratio data, though, you can also add and subtract values.
For example, if you increase the temperature from 10°C to 15°C, that is an increase in 5°C (10 + 5 = 15). This is an example of Interval data.
Similarly, a 60 year old is 40 years older than a 20 year old (60 - 40 = 20). This is an example of Ratio data.
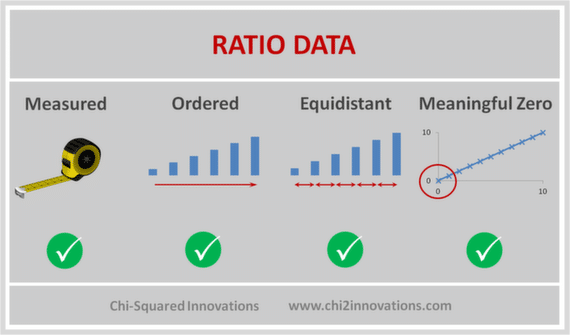
Where the Interval and Ratio measurement scales differ is that Ratio data have a real, meaningful zero and cannot be negative. This means that with Ratio data you can multiply and divide, which is something you cannot do with Interval data.
For example, a 60 year old is 3 times as old as a 20 year old (20 x 3 = 60).
This infographic will help to clarify which mathematical operations you can and can't do with each:
Nominal Ordinal Interval Ratio: Descriptive Statistics
Let's take a look at Nominal vs Ordinal data and Interval vs Ratio to see if we can find some commonalities and differences.
Nominal vs Ordinal: Descriptive Statistics
Nominal and Ordinal measurement scales have categories, and as such you can calculate the:
With Ordinal data, since their categories are ordered, you can also find the largest and smallest categories. You can't do this with Nominal data because there is no order to the categories.
You can calculate the Inter-Quartile Range of Ordinal data (if the median is the most appropriate measure of centrality), although that can prove difficult to interpret.
Have you ever tried to calculate the IQR of [Small, Medium, Large]?!??
Obviously, the more categories you have, the easier it is to understand.



Interval vs Ratio: Descriptive Statistics
Interval and Ratio measurement scales are numerical, and as such you can calculate the:
In terms of calculating descriptive statistics, there is no difference between Interval and Ratio data - you deal with them in precisely the same way.
Learn More About Statistics and Data with These Books:
Nominal Ordinal Interval Ratio: Data Visualisations
As you'll see, there are some common ways of visualising Nominal and Ordinal measurement scales, and these are very different to graphing Interval and Ratio data.
Nominal vs Ordinal: Graphs
Since the only descriptive statistics you can do with Nominal and Ordinal variables are frequencies, proportions and percentages, the only ways to visualise these are with pie charts and bar charts.



Interval vs Ratio: Graphs
To visualise Interval and Ratio variables, you can use a boxplot or a histogram. You can check the central point and variability with a histogram, but you'll need to check the boxplot to see if you have any outliers. This is why you should visualise Interval and Ratio variables with both a boxplot and a histogram.
Nominal Ordinal Interval Ratio Measurement Scales Compared - Do You Know What You Can & Can't Do With Them? @chi2innovations #dataanalytics #datatypes #statistics
Nominal Ordinal Interval Ratio: Statistical Features
Nominal vs Ordinal: Stats
As well as the simpler descriptive statistics, Nominal and Ordinal variables can also be analysed using advanced statistical methods, such as in hypothesis testing.
Both Nominal and Ordinal variables can be used in pairwise statistical hypothesis testing, either as one of the variables or both.
For example, you can use Nominal and Ordinal variables in a Fisher's Exact Test or a Chi-Squared Test, where it is tested against other categorical data.
You can also test Nominal and Ordinal variables against numerical data using a 2-sample t-test or an ANOVA.
There are some additional tests you can use with Nominal and Ordinal variables, but they are more advanced and are beyond the scope of this article. If you want to know more, you can look up the Chi-Squared For Trend Test, Ordinal Logistic Regression and Nominal Logistic Regression.



Interval vs Ratio: Stats
Once you start to work with numerical data rather than categorical data, the statistical hypothesis tests you can use are more powerful and you can have more confidence in their results.
Interval and Ratio variables are often used in statistical hypothesis tests such as the Student's t-test (aka the 2-sample t-test) and the ANOVA (versus categorical data), and in correlations such as the Pearson correlation and Spearman correlation (versus numerical data).
Statistically speaking, there is no difference between Ratio and Interval variables - you deal with them both in the same way.

UNIQUE VIDEO COURSE
In less than 2 hours
your data can be:
Nominal Ordinal Interval Ratio: Summary
When it comes to analysing data, Ratio data are the best to deal with mathematically (note that I didn't say easiest...) because all possibilities are on the table. You can find the central point of the data by using any of the mode, median or mean (arithmetic, geometric or harmonic) and use all of the most powerful statistical methods to analyse the data. As long as you choose correctly you can be really confident that you are not being misled by the data and your interpretations are likely to have merit.
And if you have numerical data that are very noisy, you can always group them in categories to reduce the noise and analyse them as Ordinal data - although you will lose some information in the process.
What you can't do, though, is convert data from the Nominal or Ordinal measurement scales into Interval or Ratio data, so bear that in mind when it comes to collecting your data.
Ratio is better than Interval, then Ordinal and finally Nominal.
Happy data hunting!
Do you have any questions about Nominal, Ordinal, Interval, Ratio data? Is there something that I've missed out?
Let me know in the comments below - your feedback will help me to improve the post and make learning about data and statistics easier for everybody!
In the next post in the series we'll take a look at what you can do with each of these 4 types of data in Statistical Hypothesis Testing.
This post forms part of a series on the 4 types of data in statistics.
For more detail, choose from the options below:



