What is a Gaussian Curve, what can you do with it, and how do you get one with your data?
This blog post will give you all the answers with lots of graphics and no complicated stats...
Ready? Let's jump right in...
“In the 21st Century it is unacceptable that almost 50% of school leavers fail to achieve average grades”
Quote from a British Politician, circa 2010-ish
When I heard this live on BBC News 24, I almost fell off my chair.
Even with the most rudimentary understanding of data and statistics this is a really stupid thing to say - and these are the people that are running the country (allegedly)!
If you’re going to quote a statistic that’s been handed to you in a report, or even if you’ve worked it out yourself, you’d better damn well understand what you’re saying. Fail to do that and you can look rather foolish on prime-time television...
This politician - name withheld to protect the idiot (also because I can’t remember who it was) - clearly didn’t have a clue what he was talking about, but he said it with such passion and conviction that the interviewer probably didn’t even notice.
Or maybe he was just sniggering quietly inside.
Why was he so wrong? Let’s have a look and see…
More...

You don't have to be stupid to be a politician, but it certainly helps...
To understand why the lovely politician was so wrong, we ought to take a look at the ‘Gaussian Curve’, find out how you get one and what you do with it.
I know what it’s like when somebody talks about distributions - your brain goes into stand-by mode and your eyes glaze over.
But stick around a little while - we’re going to look at this from the point-of-view of visualising data, not using complicated calculations and confusing stats.
I promise this’ll all be terribly easy…
Disclosure: This post contains affiliate links. This means that if you click one of the links and make a purchase we may receive a small commission at no extra cost to you. As an Amazon Associate we may earn an affiliate commission for purchases you make when using the links in this page.
You can find further details in our TCs
What is a Gaussian Curve?
Let’s take the example of the heights of school kids to find out how a ‘Gaussian Curve’ comes about.
Imagine that you go to your local school and took all the kids out of their classes (don’t actually do this - you might get arrested!).
Measure their heights and write each measurement on a tennis ball (different tennis balls, not the same one…).
Let’s say the shortest pupil is a little over 0.9m and the tallest is a little under 1.9m.
Now take 10 dustbins (if you're reading this over the pond - trash cans) and line them up next to each other in front of the playground wall. Write ‘0.9m to 1.0m’ on the left-most bin, ‘1.0m to 1.1m’ on the next bin, and continue to do this in 0.1m increments until you reach the last bin; ‘1.8m to 1.9m’.
You’ll now have 10 bins lined up from left-to-right with the following pupil height measurements written on the front:
- 0.9m to 1.0m
- 1.0m to 1.1m
- 1.1m to 1.2m
- 1.2m to 1.3m
- 1.3m to 1.4m
- 1.4m to 1.5m
- 1.5m to 1.6m
- 1.6m to 1.7m
- 1.7m to 1.8m
- 1.8m to 1.9m
Ignore the fact that there is a tiny cross-over between adjacent bins - we’re trying to keep this simple…
Now try and persuade the little darlings to put the balls into the correct bins - a difficult task, I know, but who said being a statistician was easy?
The ball labelled with 1.21m goes into the ‘1.2m to 1.3m’ bin, the ball with 1.76m written on it goes into the ‘1.7m to 1.8m’ bin, and so on.
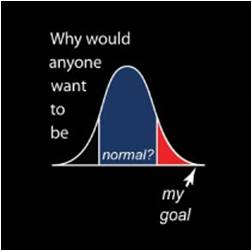
Count the balls in each bin and then paint dustbin lid-sized tennis balls above each of the bins - one for each ball counted (i.e. for each pupil). If there are a lot of school kids, we can paint one ball for each ten pupils.
You should get something that looks like this:
Count them all in, and count them all out. Otherwise a few will likely go missing...
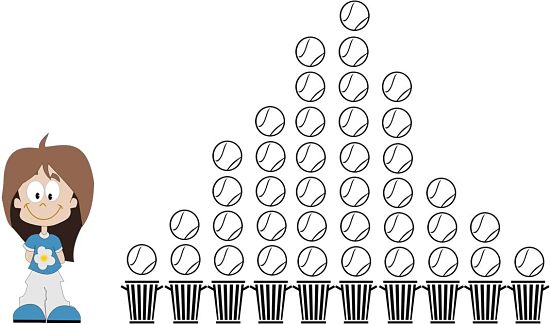
If we now measure the height of each painted stack of tennis balls - the number of school kids in each pupil height bracket - we can plot a Histogram (a vertically stacked bar-chart) that represents the height distribution of the school kids. Connecting the tops of the bars together and then smoothing them out we should get something like this:
Histogram with a fitted Gaussian Curve
As you can see, the average pupil height is right in the middle - whichever measure of ‘average’ you use - and their heights are distributed equally and symmetrically each side of the centre.
This is called a ‘Gaussian Curve’, Normal Distribution, or Bell Curve, and is typically seen throughout nature. Things that follow a Gaussian Curve are:
- Heights of people
- Blood pressure
- Body temperature
- IQ scores
- Weights and sizes of thing produced by a machine
There isn’t a standard number of bins to use when sampling data like this, but usually the number of bins to use increases with the amount of data we have.
I hope you can see that as the amount of data and number of bins increases, the smoother the Gaussian curve becomes, so if you want to describe your data accurately you should collect lots of data.
How to Lie With Numbers, Stats and Graphs
A Box Set Containing Truth, Lies & Statistics and Graphs Don't Lie

Truth, Lies & Statistics and Graphs Don't Lie are two of our biggest selling books – and by far our funniest!
In these eye-opening books, award-winning statistician and author Lee Baker uncovers the key tricks of the trade used by politicians, corporations and other statistical conmen to deceive, hoodwink and otherwise dupe the unwary.
Discover the exciting world of lying with data, statistics and graphs. Get this book, TODAY!
How to 'Read' Gaussian Curves
OK, so now we know what a Gaussian Curve is and how to recognise it, but what can we do with it?
Well, for a fixed amount of data that is normally distributed, the general shape of the Gaussian curve doesn’t change, but it may get taller and thinner or shorter and fatter.
Have a think about that for a moment - if you take a single class of pupils they’ll all be the same age and will likely all be of a similar height. The heights will have less variation - the difference between the shortest and tallest will be relatively small (the distribution will be narrow) - and there will be more pupil heights closer to the centre (the distribution will be taller).
On the other hand, if you take pupils from all classes in a school there will be a broader range of ages and greater variation in the heights. More pupils will be found in the tails (away from the centre) and fewer grouped around the average making for a broader and shorter distribution.
So the width and central point of the Gaussian curve can tell you a lot about your data.
Gaussian Curve Example
Let’s compare the heights of kids at 2 well-known fictional schools.
Imagine that you go to your local Hogwarts school and took all the kids out of their classes…
OK, so you know the drill by now - it’s exactly the same as before. You follow this drill for both Hogwarts and St Trinians.
Take the average pupil height at both schools (the central points of your Normal distributions) and plot them as a Histogram. Overlay the Gaussian Curve for each school onto the Histogram and you should get something that looks like this:
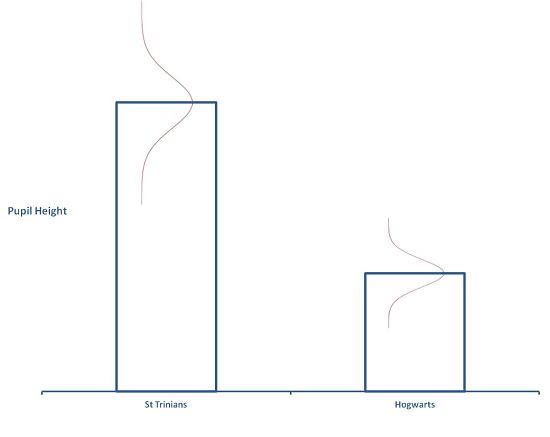
Histogram - St Trinians v Hogwarts
These bell curves don’t overlap very much. There’s certainly no overlap in their central portions, but there may be a small overlap in the tails. This tells us that there is likely to be a real difference in heights between the pupils at these 2 imaginary schools.
Related Books
Calculating Some Useful Numbers From The Gaussian Curve
So now we know how to use Gaussian curves to compare different groups in a descriptive way, but how about trying to put some numbers onto this to give us a better ‘feel’ for what is going on in the data (I’m not going to go into statistical tests, significance, confidence or p-values here - I’ll leave these for a future post).
We know that the width of the Gaussian curve is important, so let’s try to measure it.
If we take our data and line it up from smallest-to-largest, we can take the middle value to represent the centre of our data; the average height of the pupils at this school. I’m sure you recognise this - it’s called the median.
Now we have split our data in half, with exactly half of the pupils shorter than the median and half taller.
If we now take the middle value (median) of the bottom half of the data and do the same with the top half, we have now split our data into 4 parts with equal numbers of pupils in each quarter.
The central points of the lower and upper halves are called the 1st and 3rd Quartiles, often abbreviated as Q1 and Q3.
The 1st and 3rd Quartiles give you a good ‘feel’ for the width of the data distribution.
For a Normal distribution, Q1 and Q3 are equidistant from the median, but their distance from the median can vary when the data are not symmetrical (non-Normal).
So if each of these quarter-sections of data contains equal numbers of pupils, then the middle 2 quarters must contain exactly half of all the pupils. This is called the Inter-Quartile Range (IQR) and is the difference between Q3 and Q1:
IQR = Q3 - Q1
I think you can see that these measures would be very useful to show on the Histogram so that we can get a better understanding of pupil heights.
We can also plot the maximum and minimum values to show the range of heights at the school, but that wouldn’t give us much of an idea about any extreme heights (short or tall). Instead, we can decide how different a height should be before we can say that it doesn’t fit comfortably with the rest of the data. These data points are called outliers and are often calculated as being more extreme than 1.5 IQRs away from Q1 or Q3. In other words:
High Outliers > Q3 + (1.5 x IQR)
Low Outliers < Q1 - (1.5 x IQR)
When we plot these values we can immediately identify values that ‘fit’ within our dataset and the outliers that don’t.
VIDEO COURSE
Statistics:
The Big Picture
Free to try - no need to buy or register!
How Box-and-Whisker Plots Relate to Gaussian Curves
Putting together all these values into a single plot, we can show the median, Q1, Q3 and IQR as a single box, and show the limit of the values that ‘fit’ with whiskers. Outliers can be shown as individual plot points outwith the whiskers, like this:
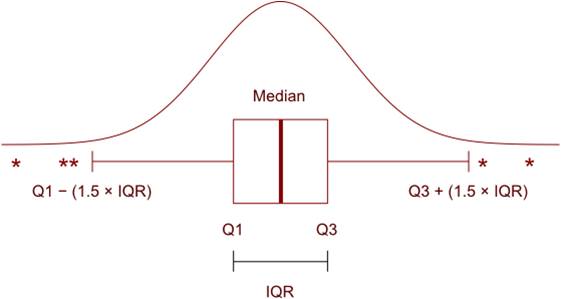
Box and Whiskers Plot with Gaussian Curve
So now we have a way of representing our data with a single image that is constructed from a few simple calculations on our data - the Box and Whiskers Plot.
Better still, we can use Box and Whiskers Plots to compare our 2 schools:
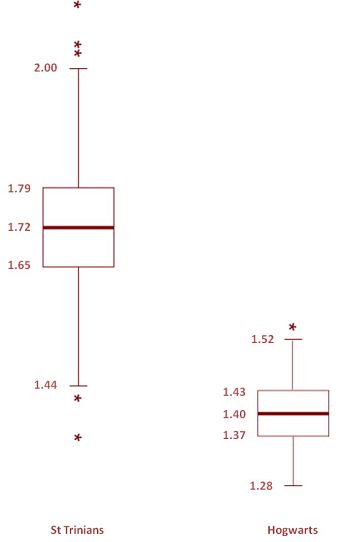
Box and Whiskers Plot - St Trinians v Hogwarts
By looking at the distribution of the heights of pupils at each of these schools in the Box and Whiskers Plots it becomes really easy to see what the average pupil heights are, and that the middle half of measurements for both schools are very different. In fact, more than 3/4 of school kids at Hogwarts would be considered as extremely short if they studied at St Trinians instead (not that they ever did any studies at St Trinians…).
Summary
So I hope that we can all agree now that the Normal distribution is, er, well, normal, and not something to be afraid of.
It is easy to understand and simple to represent with numbers and a Box and Whiskers plot to get some real insights into what your data is trying to tell you.
And to come back to the earlier point about the idiot politician and his ‘almost 50% fail to achieve average grades’ comment - I hope you understand why it was ridiculous.
The average represents the middle of the distribution. By definition, 50% of the values lie below the average, so there will always be almost 50% that fail to achieve the average no matter what the average value is.
And we wonder why politics is in crisis…
*hand slaps forehead, exclaims ‘Doh!’*
So there you have it - The Gaussian Curve laid bare and in all its glory. Easy peasy...