Bayes’ Theorem and Bayesian Statistics – Your First Steps

Bayesian statistics, or so they say, is not for the faint of heart. But is that true? At some point in their learning curve, once they’ve had a little experience, students of statistics usually come across Bayes’ Theorem and wonder if it’s something they should spend a little time studying. After half an hour or so, they realise they’ve fallen into Alice’s rabbit hole and then take a huge decision – they decide whether to press on or turn back, and for most, this decision is a permanent one.

Is Bayesian statistics really as difficult as some would have you believe?

This blog post is an introduction to Bayesian statistics and Bayes’ Theorem. Its purpose is to help you in getting started with Bayesian statistics and get over the initial fear factor. Once you start to get a bit less intimidated I’ll point you in the right direction to learn more.

So what is Bayesian statistics?

Bayesian statistics mostly involves conditional probabilities, which is the probability of an event A, given that event B has happened, and it can be calculated using Bayes’ Rule.

The basic premise is this: you make a guess on what you think your outcome will be. This is called the Prior probability. Then you collect some data and update the probability of the outcome accordingly. We call this the Posterior probability.

Sounds simple, doesn’t it?

Well, it does get a bit harder than this, and there can be some mathematics that look intimidating, but in truth you won’t need to worry about that, there are packages that do all the heavy lifting for you – Bayesian statistics is no harder than classical statistics!

Ready? It’s time to get started with Bayesian statistics!

What is Bayes’ Theorem in Simple Terms?

In short, Bayes’ Theorem is a way of finding the probability of an event happening when we know the probabilities of certain other events.

Bayes’ Theorem is named after the Englishman Thomas Bayes, an 18^th century statistician and Presbyterian minister who, interestingly, never actually published his theorem – it was published by Richard Price after his death.

The simplest way of thinking about Bayes’ Theorem is that before you have any evidence you ‘guess’ the likelihood that an event will happen, then you can improve your guess once you’ve collected some information.

For example, before opening the curtains and looking outside you can speculate on how likely it is that it will rain today. Then you open the curtains to see if there are clouds, ask your wife to count how many people are carrying brollies and check the calendar to see if you’re in the monsoon season. How did your guess go? Now that you have some data, do you want to change your mind as to how likely it is to rain today?

In a nutshell, this is what Bayes’ Theorem is all about.

Related Books

What is Conditional Probability in Bayes’ Theorem?

In probability, you can have independent events and dependent events.

Independent events are things that happen that are unconnected with each other, such as the probability that it will rain today and the probability that your brother-in-law will call to wish you a happy birthday. You can see that neither of these events are connected with the other. They are independent.

In probability, there is a probability multiplication rule that tells us that the probability of independent events A and B happening together is the same as the probability of event A multiplied by the probability of event B (in probability, when you see the word AND, you multiply), and it looks like this:

For example, if the probability of finding a parking space is 0.22 and the probability of having the correct change for the parking meter is 0.34, then the probability that you will get parked without having to frantically seek change before the parking attendant gets to your car is 0.22 x 0.34 = 0.07.

It’s not looking good!

Bayes’ Theorem, on the other hand, deals with the probabilities of events that are dependent, where one event is conditional on the other happening. For example, what is the probability that you will win the lottery? It depends. Did you buy a ticket? The probability of winning the lottery is dependent on how many tickets you bought.

So what happens when event B is dependent upon event A?

In this case, the probability multiplication rule is modified slightly to give us the conditional probability multiplication rule:

The last term in this equation means “the probability of B, given that A has occurred”, and is known as the conditional probability.

Let’s say that you wish to draw two cards of the same suit out of the pack. There are 52 cards in the pack, with 13 of each suit. If with your first pick you draw a Diamond, what is the probability that you will draw a Diamond with your second pick?

Here, drawing the first Diamond has a probability of P(A) = 13/52.

Your second draw, though, doesn’t have the same probability as your first. Now there are 12 Diamonds left in the pack of 51 cards, so the conditional probability of drawing a Diamond given that you drew a Diamond with your first pick is P(B|A) = 12/51.

So the probability that you will draw two consecutive Diamonds from the pack is 13/52 x 12/51 = 0.06.

What is Bayes’ Rule?

So if the first card you picked was the 5 of Diamonds, and the second was the Queen of Diamonds, the probability of this outcome is P(A and B) = 0.06. We wrote this as:

Now imagine the same situation, but reversed. Your first pick was the Queen, and your second pick was the 5 of Diamonds. This would be the same outcome with the same probability, wouldn’t it? Yes it would, so P(B and A) = 0.06 too, and we can interchange A and B to give us:

Knowing that it doesn’t matter whether you picked a 5 then a Queen or a Queen then a 5 means that P(A and B) = P(B and A), and if this is true (it is!), then the following is also true:

This is what is known as Bayes’ Rule and is at the heart of Bayes’ Theorem, which we can restate as (notice that I’ve rearranged it slightly):

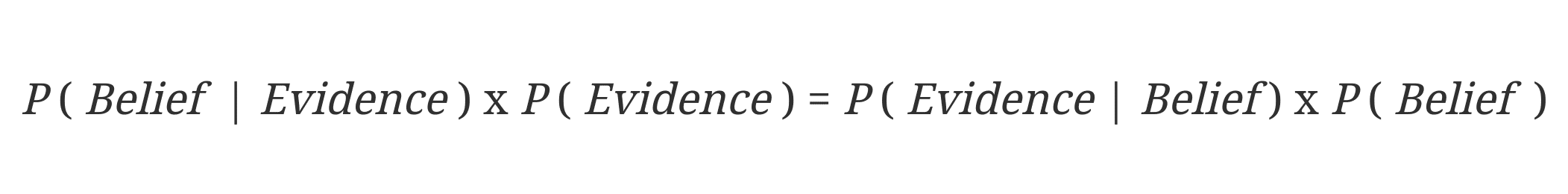
In words, we can state Bayes’ Rule as the probability that a belief is true given new evidence (that’s the first part), when modified by the evidence (the second part) is equal to the probability that the evidence is true given that the belief is true (the third part) when modified by the probability that the belief is true (the fourth part).

Related Books

What Are Prior and Posterior Probabilities?

There is a wonderful symmetry to this equation, but you don’t often see it in this form. It will usually be explained in terms of events A and B, and when rearranged looks like this:

The left side of the equation is what we know as the Posterior probability (aka the Bayesian Posterior probability), and the right side is the Prior probability (aka the Bayesian Prior probability) modified by the evidence you collected about events A and B individually.

We say that the probability that event A will happen given what we know about event B is equal to the probability that event B will happen given what we know about event A, modified by what we know about events A and B independently from each other.

You can think of this in terms of a Prior probability (the guess or the Bayesian Prior) and a Posterior probability (the improved guess), based on the evidence (the information you’ve collected).

So now when you hear people discussing Prior and Posterior probabilities, you know what they’re talking about!

Bayes’ Theorem – An Example

Let’s say that you want to go to the beach today, a random day in April, and when you wake up it is cloudy. What are the chances that there will be rain?

Let’s re-write Bayes’ equation:

To answer the question, we need to know three things about cloud and rainfall in April:

And now plug the numbers in:

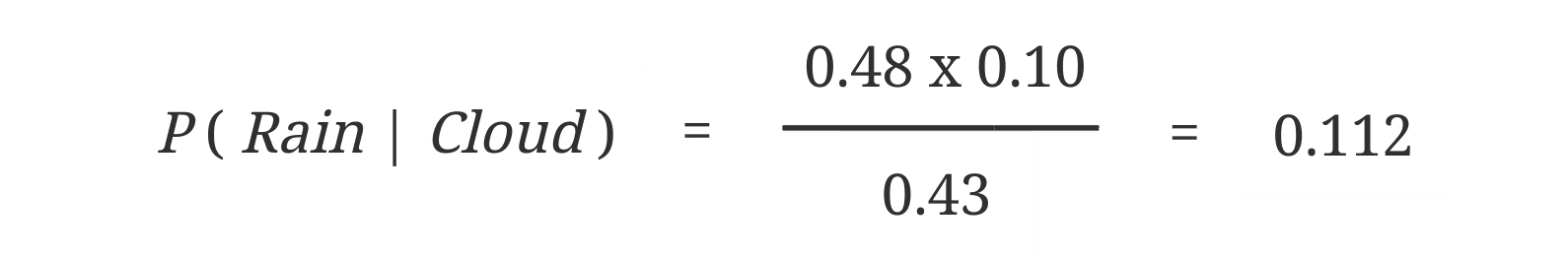
So the probability that it will rain today is 11.2%.

It looks like it’s time to head off to the beach!

How is Bayesian Statistics Different to Classical Statistics?

There is a schism in statistics, and it’s all Thomas Bayes’ fault! Maybe he didn’t publish his work because he knew it was going to cause problems…

The debate between classical statisticians (also known as frequentist statisticians) and Bayesian statisticians has been rumbling on for centuries and doesn’t look like stopping any time soon.

The difference between classical statistics and Bayesian statistics is quite a subtle one, but has huge implications from there on in.

Frequentist statistics tests whether an event occurs or not, and calculates the probability of an event in the long run.

Basically, classical statistics goes like this:

There’s nothing wrong with that is there?

Except the Bayesian will tell you that there is a huge problem with it.

Let’s take an example of flipping coins to see what the Bayesian is talking about.

The table below represents the number of Heads obtained from tossing coins a number of times:

In classical statistics, the outcome is a fixed number. In any given experiment, the probability of Heads that you calculate is fixed. What you expect, at least in theory, is that the probability of Heads will be exactly 0.5, irrespective of how many trials you run.

As you can see, it isn’t. It doesn’t matter how many times you run the experiment, you will get a slightly different outcome each time. In fact, if you have an odd number of trials you can never get a probability of exactly 0.5 (look at the middle row where the probability is 0.5 – flipping the coin one more time will give you a probability that is not 0.5, irrespective of whether the outcome is Heads or Tails).

What?!?? Either the outcome is fixed or it isn’t – it can’t be both!

If you’re a Bayesian statistician, that final column makes you feel rather uncomfortable, and for good reason.

The Bayesian statistician is right – the issue is that the result of an experiment in classical statistics is dependent on the number of times the experiment is repeated!

This is a fundamental problem for Bayesian statisticians, and is one that they solve by updating the probabilities whenever they get some new data.

In contrast to classical statistics, Bayesian statistics goes like this:

So if Bayesian statistics gets round this problem, why are frequentist statistics still the most widely used inferential technique?

Is Bayesian Statistics Better?

Yes.

And no.

It depends on who you speak to.

Classical statistics are quick and easy to compute, but interpreting the results is difficult: results are often misunderstood and reported incorrectly. Don’t believe me? Try explaining what a p-value is to your Granny!

As well as that, classical statistics often have a set of assumptions that mean that you cannot answer the question that you want to, so instead you ask a similar question and test that, hoping that the answer is ‘close enough’ to what you want.

There are loads of Bayesian statisticians that believe that there is a complete disconnect between the questions that p-values can answer in the classical statistics framework and the questions that we need answers to in the real world:

This is one of the main reasons that many choose to switch from classical statistics to Bayesian statistics.

This is what John Tukey said of classical statistics:

On the other hand, Bayesian statistics are difficult to compute, but interpreting the results is easy. One of the biggest drawbacks, though, is that the accuracy of your results are dependent on the form of your Prior distribution – if your prior knowledge is accurate, you will get an accurate result, but an inaccurate Prior will yield an inaccurate result.

What is important to any statistician is understanding your assumptions and having the knowledge and experience of reaching the underlying story of the data. Ultimately, most of the time frequentist and Bayesian statistics will give you the same answer.

Bottom line – it’s a choice, and there is no wrong or right answer in the battle of classical versus Bayesian statistics. It’s whatever you feel most comfortable with.

How Hard is it to Learn Bayesian Statistics?

If you use frequentist statistics, you don’t bother with all the integrals and heavy maths, do you? No, you use programs to do all that for you.

It’s the same with Bayesian statistics – unless you’re a world-class statistician, you probably look at Bayes’ Theorem and its equations and feel intimidated. Sure, it looks hard to learn Bayesian statistics, but these days there are packages that do all the heavy lifting for you, so once you’ve learnt the basics, the practical aspects are quite straightforward.

The bottom line is that it looks harder to learn Bayesian Statistics than classical statistics, but looks can be deceiving – learning Bayesian statistics is just as easy (or hard, depending on your point-of-view) as learning frequentist statistics!

When Should We Use Bayesian Statistics?

Let’s suppose that you run a poll of potential voters and you find that 53% of them intends to vote for candidate Joe. You compute a confidence interval of 43% to 63%, and you’ve got a p-value, 0.42. So what is the probability that Joe will win?

Under this classical statistics framework you have no idea, but under the Bayesian statistics framework you can work it out.

Bayes’ Theorem is a tool for calculating conditional probabilities (probabilities that are reliant on other things, such as ‘what is the probability that event A occurs, given that event B has occurred?’), so if the outcome you seek is a probability, then you should look to Bayesian statistics.

Bayesian Statistics – Summary

Hopefully I’ve given you a little flavour of Bayesian statistics and that you’re not put off by it. There are some clear advantages to using Bayesian statistics, but some disadvantages too. One thing I think is clear is that more and more people will make the switch to Bayesian statistics as they realise that classical statistics just can’t answer the really important questions of Life, the Universe and Everything…

Bayesian Statistics – Where To Learn More

There are lots of places online to learn about Bayes' Theorem and Bayesian statistics, and for all levels of ability.

We recommend the ones below, but there are others. If you recommend any that are not listed, let me know in the comments and I may add them here.

Bayesian Statistics Courses at Udemy

Below are a few related Udemy courses that we recommend. They are by no means the only ones - there are LOADS more, and if these don't tickle your fancy, just click through. I'm sure you'll find something that does.

*NOTE - courses at Udemy are often listed as around 100 £/$/Euro, but they have sales very often when you can buy courses for around 10 £/$/Euro. If you want to find out the sale price, just click through!

Bayesian Statistics Courses at Coursera

Learning at Coursera is great! For a lot of their courses, you can study for free and pay a small fee at the end if you want the certificate.

Below are a few related Coursera courses. They are not the only ones, just click through and I'm sure you'll find something that you like.

Bayesian Statistics Courses at Pluralsight

Pluralsight is a great place for Data Ninjas to pick up some new skills.

If you want to level up your Python, Machine Learning or Hadoop skills (there are loads more), then you might want to check them out.

They have 6,500+ expert-led video courses, 40+ interactive courses and 20+ projects, and their plans start from £24 per month. There is also a free 10 day trial for those wanting to try first.

Below are a couple of Pluralsight courses that include Bayesian statistics.

Bayesian Statistics Courses at Datacamp

Datacamp is another great place for Data Ninjas to pick up some new skills.

They currently have 335+ expert-led video courses, 14 career tracks and 50+ skills tracks, and their plans start from $25 per month. There is also a free trial that includes the first chapter of all courses for those wanting to try first.

Below is a Datacamp course that include Bayesian statistics.

Bayesian Statistics Courses - Final Word

When you've done any of these Bayesian statistics courses, please return and leave some feedback and a review in the comments below. If you loved the course, great - come and tell us. If you hated it, that's great too - leave a comment saying what you didn't like about it.

If you discover any better Bayesian statistics courses out there, let me know - I may change my recommendations!