I'm sure you all know how to do a correlation analysis to test if one variable is related to another. You probably even know when to use a Spearman correlation test over a Pearson correlation test.
But did you know that the answers from these tests are probably wrong?

Pin it for later
Need to save this for later?
Pin it to your favourite board and you can get back to it when you're ready.
When you have a pair of variables, finding a statistical relationship between the pair of them is pretty straightforward. It’s easy to see that where you have maybe a dozen variables you can analyse them pairwise using standard correlation tests and find out which relationships exist in your dataset, and which do not.
It's so simple it's enough to make you feel smug and self-satisfied - maybe even a stats hotshot.
Not so fast, cowboy – it’s not quite that simple!
You see, when you analyse a pair of variables using univariate tests, you’re testing to see whether there is a relationship between these variables without taking into account any other potential factors.
There are loads of ways in which your variables might be interacting with and influencing each other, so when you have a significant p-value from univariate analysis you can’t be sure that the answer you get is correct.
Correlations "There is one very good reason why your correlation results are probably wrong" @eelrekab #analysis #statistics
Let me make it easy for you.
If you get a non-significant p-value (larger than 0.05), you can be pretty sure (actually, 95% sure) that there is not a direct relationship between your variables. That’s not to say that one does not influence the other indirectly, it may do, but there is not likely to be an independent relationship between them.
On the other hand, if you get a significant p-value (smaller than 0.05), the best you can say is that there may be a relationship between them. The relationship might be independent, but equally it might not.
This flow chart might help you a little:
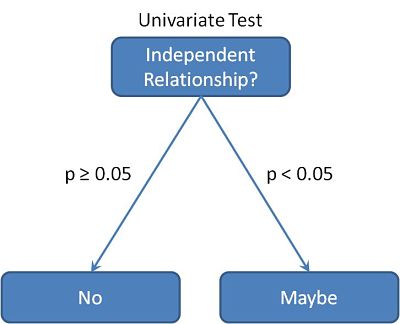
Feeling a little less smug now, aren’t we?
So if univariate tests don’t give us the answers we need, where do we go from here? Well, the univariate tests are still useful to us. Remember that univariate tests are pretty good at telling us when there isn’t a direct relationship between a pair of variables.
This is useful information and allows us to narrow the field of possibilities between what might be related to your main variable (aka hypothesis variable) and which ones aren’t.
So, in turn you test each variable against your hypothesis variable to see which of them are not related. Then you discard them. What remains are the variables that might be related to it.
The next step gets tricky because we now need to test the relationship between the hypothesis variable and all of these variables whilst taking into account all the possible interactions between them. Sounds scary!
We’re now dipping our toes into the world of multivariate analysis.
I'm not going to go into detail about univariate and multivariate correlations here because I explain all about them in my eBook Beginner's Guide to Correlation Analysis.
I will give you a little advice though: do univariate analyses on your data first to get a good understanding of the underlying patterns of your data, then confirm or deny these patterns with the more powerful multivariate analyses. This way you get the best of both worlds and when you discover a new relationship, you can have confidence in it because it has been discovered and confirmed by two different statistical analyses.
When pressed for time I’ve often just jumped straight into the multivariate analysis. Whenever I’ve done this, it has always ended up costing me more time – I find that some of the results don’t make sense and I have to go back to the beginning and do the univariate analyses before repeating the multivariate analyses.
I advise that you think like the tortoise rather than the hare – slow and methodical wins the race…
Correlation Resources
This blog post is an accompaniment to my eBook Beginner's Guide to Correlation Analysis, and is here to help you take the next steps.
Below you'll find the best resources on learning about correlations that we've found on the web, and we update it frequently with new books, video courses, software and whatever else we can find (and create ourselves), so feel free to bookmark us, share us on the web and call in regularly to top up your correlation ninja skills.
Disclosure: This post contains affiliate links. This means that if you click one of the links and make a purchase we may receive a small commission at no extra cost to you. As an Amazon Associate we may earn an affiliate commission for purchases you make when using the links in this page.
You can find further details in our TCs
Books
Video Courses in The Hive
The Hive is our online learning portal where you can find courses on data analysis, statistics and machine learning.
Unlike other online course platforms, we actively encourage networking and collaboration, and The Hive is a place where you can chat and make friends in our exclusive members-only built-in social media community. You can also contact me and tell me what courses you need - I am in the habit of taking requests and creating personalised video courses!
In The Hive there are plenty of FREE courses (get a free plan to access these), and you can access the most in-depth courses for a small monthly or annual subscription (or purchase courses individually). Better still, each of the premium courses has a shortened free version so you can try-before-you-buy.
If you want access to exclusive, personalised content, then The Hive is the place to be!
VIDEO COURSE
Statistics:
The Big Picture
Free to try - no need to buy or register!
Udemy Video Courses
Udemy is a great place to learn new stuff, not just about data, stats and AI, but about making model trains, how to apply make-up and, oh, just about anything else you can think of.
Courses (when they're on sale, which is very often) are typically priced at about 10-15 £/$/Euro. The upside is that the courses are very cheap, and usually very good. The downside is that courses aren't part of any formal programme, so you won't get any kind of certification.
If you want to fill gaps in your education or even learn whole topics, then Udemy is a great place to go.
*NOTE - the prices listed below are the full price, and are not automatically updated when a sale is on. If you want to find out the sale price, just click through!
Coursera Video Courses
Coursera offer a more considered approach to learning and offer individual and full degree courses, and you get certificates too that you can display on your LinkedIn profile to impress your future boss.
Prices are usually around the 50 £/$/Euro mark per course.
The great thing about Coursera is that all courses are taught by University professionals, so you know that these guys are the best and brightest in their field. On the downside, these courses are quite intensive and you need to be able to set aside a fair chunk of your time over a few weeks to complete the course. Unless you enjoy pulling all-nighters...
Software

CorrelViz - All The Correlations in Your Data In Minutes, Not Months
Discover new insights - Save time and money

